さて，今回は大好評の「暗記しない数学シリーズ」です!!
数学Bで出てくるΣ(シグマ)の公式についてです．
このシグマ公式を，図形を使って解説してみようと思います
シグマの公式が覚えられないと悩んでいた高校生も，こう説明してあげたら一瞬で理解していました．
シグマがわからなくて悩んでる高校生，昔ならった大人の方，誰でも楽しめる内容になっています!!
シグマ公式ってなんだ？
さて，まずシグマってなんだ？ってところからの方もいらっしゃるでしょう．
教科書をめくるとこんな公式が．
ぱっと見難しそうですよね．
[voice icon=”https://cdn-ak.f.st-hatena.com/images/fotolife/M/McG/20180616/20180616133321.png” name=”迫” type=”l”]
見た感じ記号が多くて難しそう…
この式覚えるの辛そうだな…
[/voice]
と，高校生の時の僕も例外なくこんな感じでした．
でも，実際のところシグマ公式って全然難しくありません．
実は，ただ足し算をするだけです．
例えば，「1+2+3+4+5を計算しろ」って言われたら小学生でも答えられます．
それをシグマを使って書き表すと以下のようになります．
そう，シグマ表記さえできれば，あとは公式に入れるだけで計算が可能になるというわけです．
これだけだとありがたみがわからないと思います．
例えば，「1〜10000まで全部足して!!」と言われたら，普通に計算したらとてもめんどくさいですが，シグマ公式を使えば一瞬です．
もちろん，電卓を使ってがんばって足し算で計算したものとシグマ公式を使って求めた答えは一致します．
さて，問題になるのはいかにして公式を覚えるかですね．
ここからが本番です．
1〜nまで足すことを図形的に表現してみる
さて，例として，1〜nまでを足してみることを考えましょう．
一本のテープが置いてあり，そこに1〜nまでの数字が書かれているとします．
1〜nまでの数字を合計を求めるのは，このテープにかかれている数字の合計を求めるのと同じというわけです．
このテープと同じものを用意して，ひっくり返して重ねてみます．
すると，n+1がn個出来ました．
n+1がn個出来たということは，2本を重ね合わせたテープに書いてある数字の合計はn(n+1)となります．
1本のテープの和はそれの半分ですね．
ということで，\(\displaystyle\sum_{k=1}^{n} k=\frac{n(n+1)}{2}\)が導けました．
2乗和を図形的に理解してみる．
さて，次は2乗の和です．
いきなり一般化ですが，「1〜nまでの2乗の和を計算せよ」と言われたらどうしますか？
これは，こういうことです．
これだとちょっと方針が立ちづらいので，これを足し算だけで表してみます．
お，なにやら階段状になりましたね．
つまり，これって2乗の和って単純にこう考えられるわけです．
この三角形を時計回りに120度回転，反時計回りに120度回転させた三角形を考えてみます．
ここで，あることに注目してみましょう．
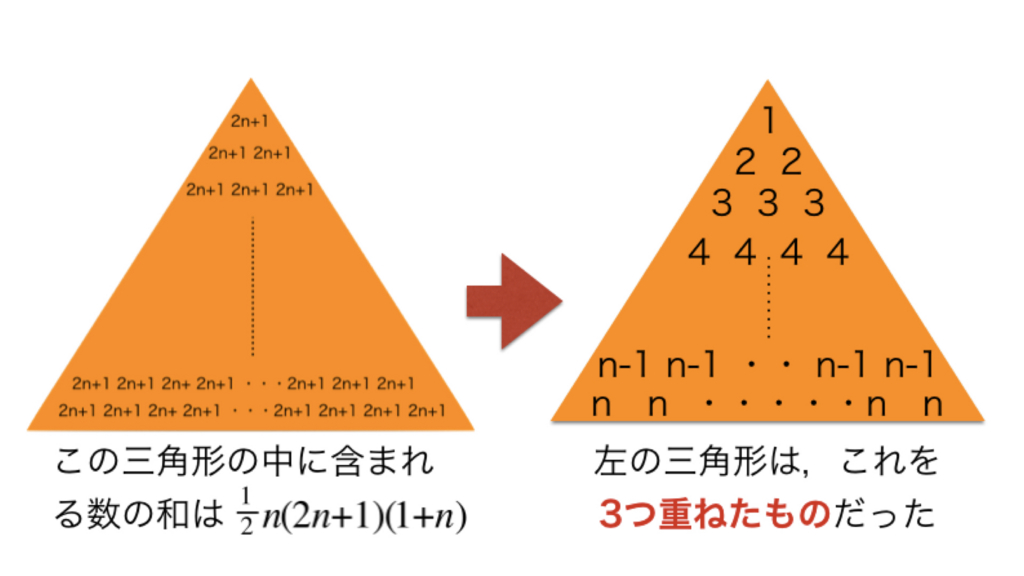
これ，よく見ると同じ場所同士足してみると全部2n+1になるんです．
つまり，この3枚を重ね合わせてみると，2n+1がいっぱい入った三角形ができます．
ということで，この三角形の中にある2n+1の数を求めてみます．
この三角形の1段目には1個の2n+1が，そして2段目には2個…
つまり，この三角形全体にある2n+1の数は，さっき求めた1〜nまでを足し合わせるシグマ公式を使って求めることが出来ます．
三角形全体にある2n+1の数がわかったので，2n+1にその数をかけてあげれば三角形の中にある数の合計がわかります．
今扱っている2n+1がいっぱい入っている三角形は，2乗の和からスタートした最初の三角形を回転させて3枚足したものでした．
つまり，3で割ってあげればもとの三角形の中に書かれていた数字の和が出ます．
ということで，2乗の和の公式\(\displaystyle \sum_{k=1}^{n} k=\frac{1}{6}{n(2n+1)(n+1)}\)を導くことが出来ました．
こうやって，自分で導いた公式は忘れたとしても数十秒あれば頭のなかで組み立てて思い出せます
このようにして論理だてて考えていくプロセスがすごく大事なんじゃないかなと実感するこの頃です．
追記
「3乗公式も見たい!!!」とのことだったので3乗の和の公式でも図形的解釈をやってみました!!
長くなってしまうのでこの記事に追加ではなく，別記事として更新しました．
- 日本一わかりやすい「経済的自立を果たす人生攻略の10ステップ」（33分23秒）
- 見るだけで売上3倍は確実。「時給10円から年商10億」に至るまでの全ての道のり（39分15秒）
- 有料講演会の内容を公開。最短最速で0→1を立ち上げる起業術（1時間08分35秒）
- 起業初心者へ向けた即金で10万円を稼ぐ具体マニュアル（PDF24ページ）
- 資本主義社会においてお金持ちになる5つのルール（17分36秒）
