こんにちは，学生エンジニアの迫佑樹(@yuki_99_s)です．
中学，高校，大学と理科や物理を勉強していると，様々な公式を習ってきたと思います．
1通りいろんな公式を習った後で，まとめてみると物理法則の美しさを感じることが出来るはず．
物理履修者であれば高校生でも理解できるはずなのに，大学で微分方程式の授業を受けるまで習わないのはもったいないということで，今回軽くまとめてみました
微分の知識が必要なので，はじめに軽く微分について触れてから，本題へ進んでいきます．
対応関係を整理すると，見えてなかった関連性が見えてきてとっても楽しいですよ．
時給と微分
さて，「微分」と聞くと高校数学のボス的存在で「とても難しいもの」という印象がある方も多いのではないでしょうか？
微分っていうのは，物事がどんなふうに変化するかというのを表したものなので，概念的にはそこまで難しいものではないのです．
簡単に微分の概念を理解してもらうため，時給1000円でアルバイトをしている大学生を例に出してみます．
この大学生が，1時から5時までの4時間アルバイトした場合，所持金の増加量4000円ということになりますね．
さて，これをもっと数学っぽく扱うため，時刻tにおいて，所持金がx(t)円であると考えてみます．
つまり，1時の段階での所持金はx(1)で，5時の段階での所持金がx(5)ということ．
1時から5時までの4時間アルバイトした場合，5時の段階での所持金x(5)と1時の段階での所持金x(1)の差が4000円ということなので，数式で表すと以下のようになります．
今回は具体例を使って考えてみましたが，これをさらに一般化してみましょう．
『時刻tから，Δt時間アルバイトした時の所持金の増加量』は，以下のように数式化することができます．
ここで，右辺のΔtを左辺に移項してみましょう．
そして，この移項後の式において，Δtを0に近づけていったものが微分の定義です．
左辺の\(\frac{dx(t)}{dt}\)というのは，x(t)のtによる変化量を表しており，数学的にはx(t)をtで微分するという意味になります
今回の例だと，『資産』の『時間経過』による変化量を表しているということになります．
時給というのは，『所持金が1時間あたりどれくらい変化するかを表した量』という風にも言えるので，『微分というのはものがどんなふうに変化するのかを表しているだけ』という先ほどの説明と一致しますね．
たまに，数学嫌いな高校生が「微分なんて役に立たない」なんて言ってますが，微分が変化量を表すということさえわかれば，微分を使って物事がどんなふうに変化をするかが分かれば，未来を予想できるということまで理解でき，すごさがわかるはず．
今回の例だと，時給さえわかれば4時間後には自分の所持金がいくらになっているかの予想がでるというわけです．
もっと一般的に使われてる例だと，『微分を使って天気の変化を表現し，天気予報に使う』とか『ある期間の人口の変化量から将来の人口を予想する』といった感じで様々なところで使われています．
微分の計算等はとりあえず置いておき，本題に入っていきましょう．
とにかく今は，『微分は変化の量を表している』ということだけ押さえておいてもらえればOKです．
変位，速度，加速度
高校物理で初めの方に習うものが，変位と速度と加速度の関係です．
速度とは，単位時間あたりの変位の変化量であり，加速度とは単位時間あたりの速度の変化量なので，変位を時間で微分すると速度に，速度を時間で微分すると加速度になるということです
そして，この加速度や速度，変位にまつわる公式は，例えばこんなものがありました．
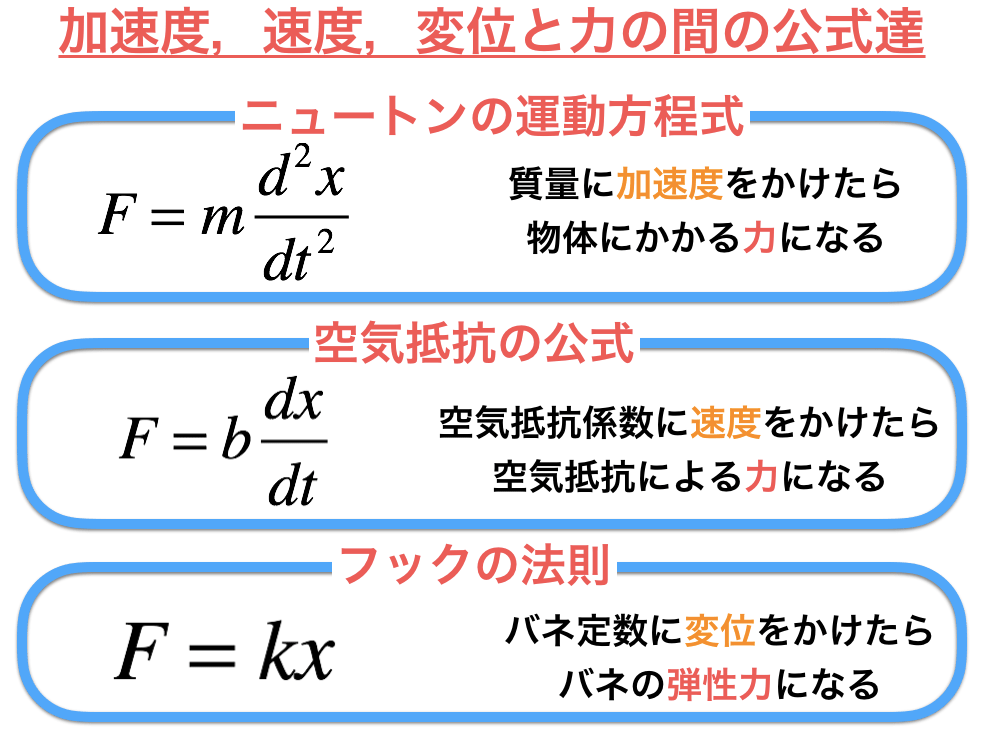
加速度や速度，変位にそれぞれ質量や空気抵抗係数，バネ定数をかけてあげれば力になるという公式です．
電気でも同じような考えで，全く同じ形の公式が出てきたとしたら，綺麗だと思いませんか？
電気回路
さて，それでは電気回路でも同じように微分を考えてみましょう．
高校物理で習うもので，「電流とは電荷を時間微分したものである」というものがありました．
先ほどの力学での変位や速度，加速度と照らし合わせるため，電荷の2階微分まで考えてみましょう．
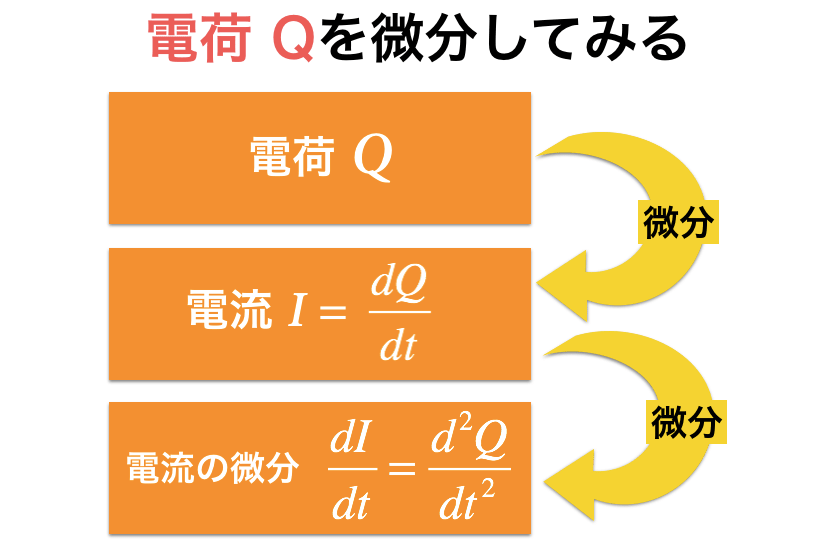
ここで，力学での力Fに相当するものは電気ではなにになるでしょうか．
実は，電圧Vが力学での力Fに相当します．電圧とは，回路に電気を流そうとする力のようなものだからですね．
この電圧と，電荷，そして電荷を1階微分した電流，電荷を2階微分したものを結ぶ公式が，力学の時同様に存在しています．
参考までに，先ほど見た，力学で出てきた公式と，電気で出てきた公式を比較してみるとこうなります．
びっくりするくらい一緒ですね．
微分方程式を習った方なら1度はこの美しさに触れているはずです．高校生くらいで扱っても全然いいと思いますけどね，公式丸暗記なんてさせるくらいならコッチのほうが良いはず．
さて，最後にこの2つで出てきた物理量たちを表にしてまとめてみるとこのようになります．
初めてこれを理解した時，「あ，電気だとインダクタンスってイメージしにくかったけど，力学でいう質量に値するのか!!」と結構感動したものです．
他にも力学や電気で様々な公式を学びましたが，いろんなものが対応関係にあります．
例えば，「コイルに蓄えられるエネルギーってなんだっけ…」とか，「コンデンサに蓄えられるエネルギー忘れた…」とかなった場合でも，この対応関係さえ頭に入っていれば2秒で導出できてしまうというわけです．
まとめ
今回は力学と電気の対応関係をみてみました．
微分を使うことで，高校の時はただ意味もわからず暗記していた公式達をこれだけ綺麗に整理できるっていうのは感動しませんか？(私だけでしょうか)
ここで言いたかったのは，ただ力学と電気の対応関係を見てほしかったわけではありません．
勉強する時は，このように対応関係を考えることでぐぐっと理解も深まるし，勉強自体が楽になるということを言いたかったんです．
もし，闇雲に公式暗記を行ってる人は時間が経てば忘れまてしまいますが，対応関係を押さえて，イメージしづらい電気関係のことを力学に照らし合わせて直観的に理解できた人は，忘れることなく，応用も簡単というわけです．
今回はたまたま直線運動と電気回路の対応関係も扱いましたが，工学系の大学だと習う，回転運動についても全く同様のことがいえます．
回転運動の場合，力に対応するのがトルクで，変位に対応するのは角度となります．
こちらも，ニュートンの運動方程式のように回転運動の運動回転運動というのがあり，全く同じ形で表されることがわかりますね．
私も，初めて慣性モーメントについて大学で習った時，「慣性モーメントっていきなり出てきたけどなんだこれ…？」ってなりましたが，「回転における質量のようなもの」というイメージさえあれば簡単に理解できたはずなのになと今になって思います．
もちろん力学と電気なので，物理的意味は全く異なりますが，数式にした時に同じ形になるというがすごいところ．
断片的に勉強していたものがパズルのようにつながっていき，関係ないと思っていたものが対応関係になっていることがわかった時，とても楽しくなります．
余談 シミュレーションの語源
余談ですが，昔の人は建造物などを作る時，建物が壊れないかを検証するために電気回路を組んだそうです．
先ほど見たように，力学系と電気回路では同じ公式が成り立ち，対応関係があるわけなので，人員やお金がかかる建築作業をする前に，手元で電気回路を組むことでシミュレーションをしていたとのこと．
今でこそシミュレーションはコンピュータでやっていますが，昔は対応性とか類似性を使っていたわけですね．
シミュレーションの語源が『似ている』という意味のSimilarという英単語であるというのも納得です．深い．
- 日本一わかりやすい「経済的自立を果たす人生攻略の10ステップ」（33分23秒）
- 見るだけで売上3倍は確実。「時給10円から年商10億」に至るまでの全ての道のり（39分15秒）
- 有料講演会の内容を公開。最短最速で0→1を立ち上げる起業術（1時間08分35秒）
- 起業初心者へ向けた即金で10万円を稼ぐ具体マニュアル（PDF24ページ）
- 資本主義社会においてお金持ちになる5つのルール（17分36秒）
