私には,中学生の妹がいるんですが先日,こんな会話をしました.
[voice icon=”https://yukisako.github.io/blog/sister.png” name=”妹” type=”l”]
明日数学のテストなんだけど,答えが合わないの!!
展開のこれ!!
わかんない!!
[/voice]
[voice icon=”https://cdn-ak.f.st-hatena.com/images/fotolife/M/McG/20180616/20180616133321.png” name=”迫” type=”l”]
わかったわかった
\((a+b)^2\)って,\(a^2+2ab+b^2\)だよね?
\(a^2+ab+b^2\)になってるよ,全部!!
[/voice]
[voice icon=”https://yukisako.github.io/blog/sister.png” name=”妹” type=”l”]
あ,そんな簡単なところだった!!
公式を覚え間違えてた!!
ありがとう!!
[/voice]
[voice icon=”https://cdn-ak.f.st-hatena.com/images/fotolife/M/McG/20180616/20180616133321.png” name=”迫” type=”l”]
ちょっと待って!!
数学は公式を覚えて解ければいいって思ってない?
数学は暗記科目じゃないよ!!
[/voice]
ここから,僕が少しばかりの解説を入れてあげると,妹の顔がぱっと変わりました.
目次
今回の例に見る良くない教え方と良い教え方
今回は,例として中学2年生で習う2乗の展開公式を出します.
義務教育で習うものですが,昔過ぎてもうわすれてしまった方も多いと思います.
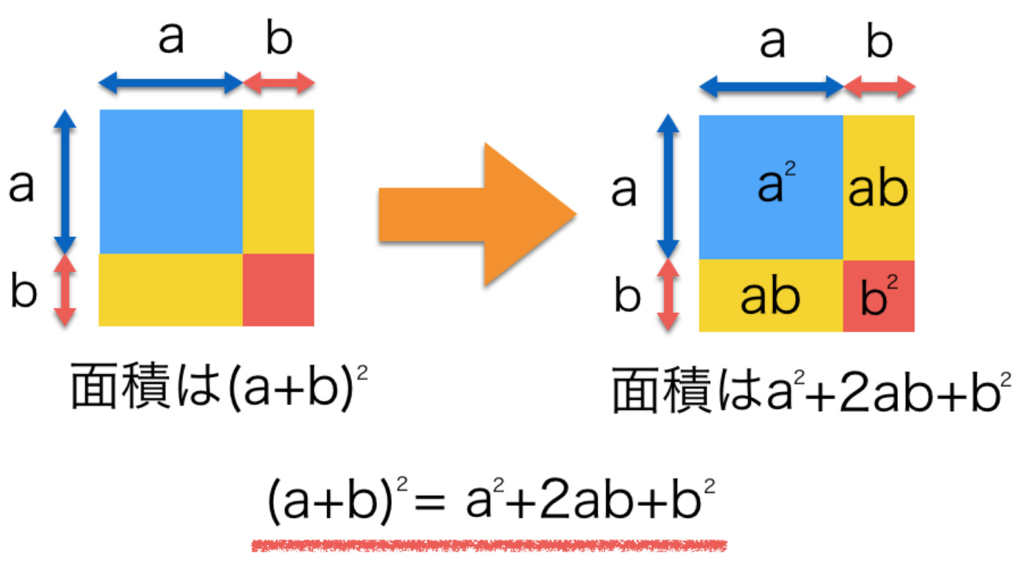
上でも少し言いましたが,\((a+b)^2 = a^2+2ab+b^2\)という公式です.
最悪な教え方
最悪な教え方は,丸暗記です.
[voice icon=”https://yukisako.github.io/blog/teacher.png” name=”先生” type=”l”]
\((a+b)^2\)は\(a^2+2ab+b^2\)になるよ
公式だから覚えよう
覚えれば問題は解けるよ!
[/voice]
点数を取らせたい塾の講師や,どう教えていいかわからないバイトの家庭教師.
ひどいときには,学校の先生まで,「とりあえずこれは公式だから覚えなさい」
それだけ言って,ひたすら問題を解かせて,出来た気にさせます.
「数学は論理的思考力を身につけるための科目!!」とか自分で言っておきながら,結局丸暗記しているだけという状況.
それではその瞬間は対応できても,すぐに忘れるし,応用もできません.
展開でしっかり理解しておけば,その後の因数分解もなにも苦労することなくスイスイ進めるのですが,ここで暗記に走ってしまうと癖がついてしまい,理解することをしなくなってしまいます.
一応,その瞬間は公式を使うだけで解けるので,出来た気にはなりますが,公式を勘違いして覚えていてテストで大惨事なんてことにもなりかねません.
マシな教え方
最低限,こんな簡単な展開公式くらいは,導出を一回はやってみるべきだと思います.
\((a+b)^2\)っていうのは,\((a+b)(a+b)\)っていうことです
なので,掛け算のルールにしたがって,これを計算していけば良いんですね.
\((a+b)^2 = (a+b)(a+b) = (a^2 + ab + ba + b^2) = a^2 + 2ab +b^2\)
わずかこれだけで,導出できます.
実際にはもう少し丁寧目に教えてあげると良いと思います.
こうすることで,公式に頼らず,「忘れても自分で公式が作れる」という思考を作ることが出来ます.
また,公式は「気づいたら覚えて使いこなせていた,意味も理解してるしいつでも導ける」という理想的な状態ができます.
論理的思考力をつけさせるという観点から見ても,丸暗記よりも数倍良いのではないでしょうか.
一歩進んで,例示してみる
ここで,中学生は思うのです.
[voice icon=”https://yukisako.github.io/blog/sister.png” name=”妹” type=”l”]
こうすると,なにが嬉しいの?
こんなの勉強してどうなるの?
[/voice]
それはたしかにそうですね,よくわからない公式を覚えさせられるのですから.
そこで,どういう時にこれが有用なのかを説明してあげます.
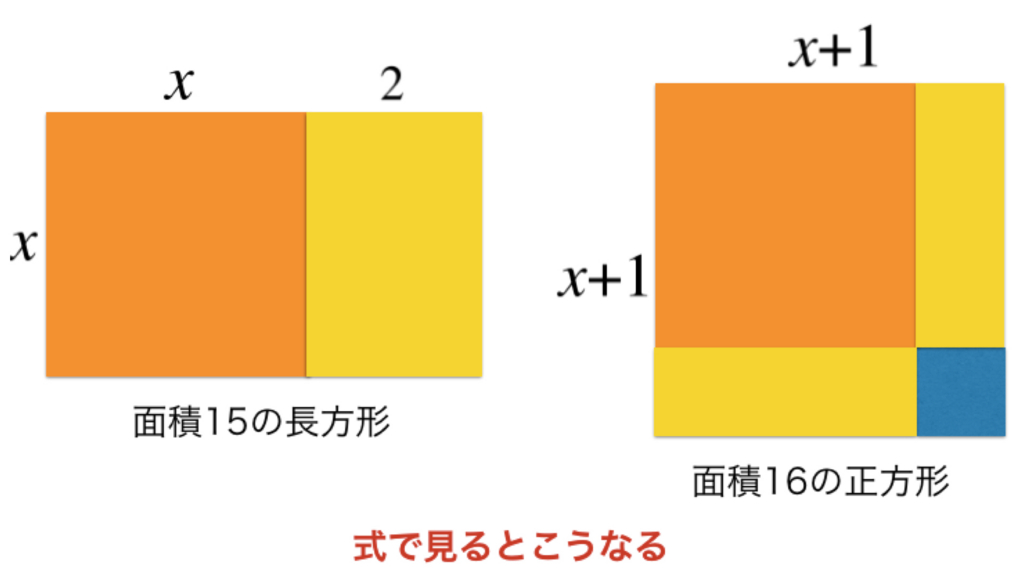
例えば,102×102,つまり102の2乗を計算しろとか言われたときのことを考えましょう.
電卓なければ,めんどくさい計算をしなければいけません.
ここで102っていうのが,100+2であることを利用します.
展開公式を使えば,\((100+2)^2= 100^2 + 2 \times 100 \times 2 + 2^2=10000+400+4=10404\)と,筆算しなくても簡単に計算することが出来ます.
このように,例を提示してあげれば,当たり前ですが学ぶ意欲もぐっと高まります.
さらに一歩進んで,図で一発理解させてみる
個人的に,勉強する時に理解がぐっと深まるのは,図を書いて視覚的に理解することが出来たときだと思います.
僕が妹にやってあげたのはこれです.
2乗と聞いて,一番身近なのはなんでしょうか?
正方形の面積が中学生にとって一番イメージしやすく,身近なのではないでしょうか?
例えば,1辺の長さがaの正方形の面積は\(a^2\)になりますね.
では,1辺の長さが\((a+b)\)の長さの面積はもちろん, \((a+b)^2\)になります.

これを,それぞれのブロックに分割してみましょう.
この青い正方形の面積は,\(a^2\),黄色い長方形の面積は,\(ab\)で,それが2つ,そして赤い正方形の面積は\(b^2\)です.
全体の正方形の面積は,その小さい正方形・長方形の面積の合計になります.

こう考えれば,一発で大抵の子は理解します.
面積は,視覚的にしっくりくるので,すっと自然に理解することが出来るのです.
暗記に走ってしまう理由
暗記に走るのは,教える方にとってはめちゃめちゃ楽です.
自分が理解してなくても,覚えろというのは誰でもでいますからね.
ただ暗記させれば点数は取れるので,見た目上は理解してる子との差もないように見えます.
この暗記型の教育スタイルって,落ちこぼれを出さないという点に関しては最適なんですよね.
日本は,戦後からずっと,先生1に対して生徒が30,40人という1対多の教育をしていました.
その教育方法だと,一人ひとりの理解に合わせて,数式の意味を理解させるなんて不可能わけです.
日本はこれまで,全員が読み書き計算ができるようになる教育をしてきました.
それが暗記型教育なんです.
もちろん,ある程度のレベルまではそれも大事です.
しかし,今,AIが発達してきているこの時代.
暗記,単純計算ならばコンピュータが人間の数万倍の速さでこなしてみせます.
やっぱり,簡単な計算にとってしても,その意味や,使いどきを考えながら指導していくのが,その子のためであり今後につながるのではないでしょうか.
少し脱線してしまいましたが,暗記に走るのは,先生の力不足,もしくは生徒を見れていない,古い教育方式から抜けられていないことが原因なわけです.
暗記型教育の弊害
中学・高校・大学と進むに連れて,必ず暗記では対応できない状況が出てきます.
例えば,小学校の割合計算.
くもわとかいうよくわからないものを導入されて,「この方法を使えば問題を解けるよ」と言われなかったでしょうか?
はじきとかきはじ,とか「キティちゃんのはじ?」なんて覚え方のもありましたね.

わからないところを隠せば,答えが出るという道具.
例えば,割合がわからないときは,割合のところを隠せば,比べる量÷もとにする量が出現するので,割合が求められる.
確かに答えは出ます.
ですが,小学生の時の僕はイマイチしっくり来ていませんでした.
なぜそこでその計算をするかが全くわからなかったからです.
全くその時は意味を理解してなく,しかし問題は解けたので理解できた気にはなっています.
暗記というツールを使い,割合を理解することなくで乗り切った子は,高校で三角比がわからなくなります.
sin?cos?なにそれ?ってなります.
三角形の斜辺に対する割合でsinやcosは定義されているからです.
ただ,しっかり割合の概念を暗記ではなく感覚的に体得していれば,全く問題なく理解することが可能です.
三角比がわからないと,三角関数がわからなくなります.
三角関数がわからないと,理系進学は不可能です.
速さ,時間,距離の概念をしっかり理解せずに暗記した子は,高校物理なんてついていけるわけがありません.
下手すれば,中学の等速直線運動が理解できずに理科嫌いになっていきます.
高校で習うことよりも,中学で習うこと,中学で習うことよりも小学校で習うことのほうが大切なんです.
そこで,暗記という手を使ってごまかした人は,どんどんわからなくなっていってしまう,負のスパイラルに入るのです..

教育上,一番伸びるのって成功体験だと思う
どんな科目においても言えることって,「成功体験があると人は伸びる」これに尽きると思います.
運動会で一番になれば,その子はスポーツが好きになります.
字が綺麗にかけたね!って褒められたらもっときれいな字で書こうとします.
私達も一緒で,ブログから1000円でも収入が出たら,「もっと稼げるかも」とどんどん記事を書きます.
よくわからない公式を覚えさせられて,なんとなくで問題が解けて成功体験が生まれるわけがありません.
「できた!」「わかった!」という成功体験を与え,どんどん得意を伸ばしていく,それが大切だと思います.
まとめ
- 数学は暗記科目 そうやって勉強すると,いつか理解が出来なくなってしまう時が来る
- 小学校の時から,とりあえず暗記で乗り切るという癖がつくような教育をされてしまっている
- 大学レベル(理系)の数学になると,暗記で対応するのはもはや不可能
高校まではめちゃめちゃできても,大学にはいってからいきなり,わけがわからなくなってしまう人も多いです.
本当に,できるだけ早くに,しっかり理解する癖をつけておくと,いろいろなこと(数学にかかわらず)を早く理解することが出来るようになります.
理解できると,数学ってとってもおもしろいですよ