こんにちは，学生エンジニアの迫佑樹(@yuki_99_s)です．
高校生の方たちがががんばって覚える公式の１つである加法定理．
$$\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$
$$\cos (\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta$$
こんなやつですね．
某先生がこんな教え方をしているのを見たことがあります．
[voice icon=”https://cdn-ak.f.st-hatena.com/images/fotolife/M/McG/20180614/20180614112223.png” name=”教授” type=”l”]
sinの加法定理は，咲いたコスモスコスモス咲いた
cosの加法定理は，コスモスコスモス咲いた咲いた
[/voice]
絶対わすれるでしょ．
三角関数の加法定理は，文系でも理系でも，誰しもが高校で習うんですが，意外と図形的な意味を理解してる人って少ないんです．
ということで，今回はこの，加法定理を折り紙を使って理解してみましょう．
折り紙を使った証明
例えば，下にこんな折り紙があると考えます．
これを，真ん中あたりで折ってみましょう．
すると，以下のようになりますね．
ここではわかりやすいように，表と裏が違う色の折り紙を使っています．
折り目の長さが1だったとして考えてみましょう．
この青い部分の三角形だけ抜き出して考えてみましょう．
以下の図のように，折った角度が角\(\alpha\)だとすると，青い三角形の各辺の長さは以下のようになりますね．
今は，青い部分の三角形だけを抜き出したので，元の場所に戻してあげます．
以下の図に示す場所を角\(\beta\)とします．
小学校で，「三角形の3つの角の和は180°」と習ったと思います．
つまり，それを使うと，以下の図の緑色で示したところは，\(180-90-\beta\)度ということになります．
では，以下の黄色で示した部分の角度はいくつでしょうか．
小学生でもできる計算ですが，「180度から，緑の角度と90度を引いたものですね．
緑の部分は，\(180-90-\beta\)度だったので，黄色の部分の角度は，\(180-90-(180-90-\beta) = \beta\)となります．
つまり，当たり前ですが，黄色の部分の角度は\(\beta\)となります．
よって，角度を図示すると，以下のようになります．
では，次に左上の三角形を抜き出して，各辺の長さを考えてあげましょう．
この三角形，斜辺の長さが\(\cos\alpha\)なので，各辺の長さは以下のようになります．
右の三角形も，同様に斜辺の長さが\(\sin\alpha\)なので，各辺の長さは以下のようになります．
これで，ようやく必要な長さがすべて揃いました．
実際に加法定理を求めていく
今回求めた長さをすべて書き込んでみると，以下のようになります．
この図で，\(\sin(\alpha+\beta)\)はどこかを図示してみましょう．
すると，\(\sin(\alpha+\beta)\)は， \(\sin \alpha \cos \beta\) と \(\cos \alpha \sin \beta\)の和であることがわかります．
では，cosの加法定理を示してみましょう．
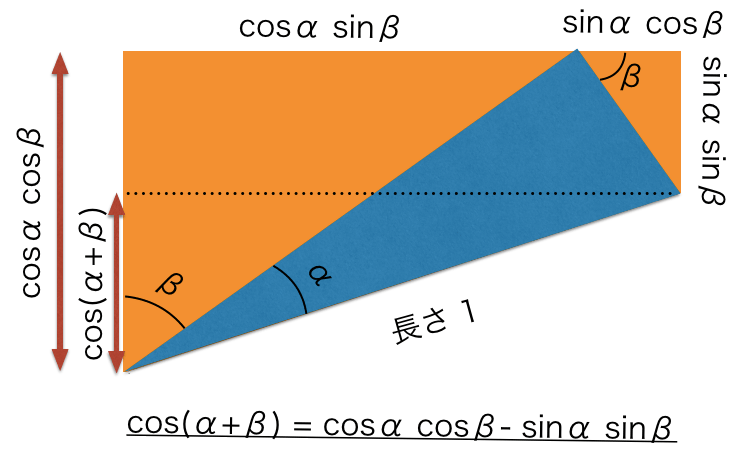
sinのときと同様にして，\(\cos(\alpha+\beta)\)の場所を図示してみます．
すると，\(\cos(\alpha+\beta)\)は，\(\cos \alpha \cos \beta\)と\(\sin \alpha \sin \beta\)の差であることがわかります．
よって，めでたくこの2つを示すことが出来ました．
\(\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta\)
\(\cos (\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta\)
もちろん，このくらいは覚えておくことが望ましいですが，ふとした瞬間に「あれ？符号なんだっけ？」とか，「どっちがsinでどっちがcosだっけ？」とかなってしまうわけです．
簡単な図ですし，一回納得しておけば試験前の安心感も全く変わってくるものです．
- 日本一わかりやすい「経済的自立を果たす人生攻略の10ステップ」（33分23秒）
- 見るだけで売上3倍は確実。「時給10円から年商10億」に至るまでの全ての道のり（39分15秒）
- 有料講演会の内容を公開。最短最速で0→1を立ち上げる起業術（1時間08分35秒）
- 起業初心者へ向けた即金で10万円を稼ぐ具体マニュアル（PDF24ページ）
- 資本主義社会においてお金持ちになる5つのルール（17分36秒）
