最近は，「プロブロガー」と呼ばれる人も増えてきました．いわゆるブログだけで生活している人．
そんな中，よく受ける質問がこれ『ブログのPV数が全然増えない』『ブログから全然収益が出ない』ということ．
こういう時は，続けていて本当に結果が出るのかどうかを数学の力でシミュレーションしてみましょう
※ほぼほぼネタ記事なので数学的モデルを作る際，大胆な仮定と簡略化を行っています．ご了承ください．
目次
未来を予想できるって？
『数学を使えば未来を予想できる』ということに，多くの人は疑問を持つかもしれません．
ただ，僕たちはそれを小学校の時に習う算数ですでに体感しているんですよ．
『時速5キロで3時間歩いたらどうなる？』みたいな問題があったと思います．
普通「15km進んでる!」に即答することが出来るはず．
これは，「3時間後にどれくらい進んでいるか，未来を予測できた」ということになりますね．
中学生的に言うと，『進んだ距離xは，経過時間tに比例しており，x=5tと書くことが出来る』というわけなので，同じ速度で歩き続けた場合，未来のある時刻においてどこにいるかをきっちり予想することが出来るというわけです．
つまり，ブログのPVや収益と経過時間の関係を数式で表してあげれば，今後どのようにPVや収益が変化するかを予想することが出来るということになります
ブログの収益をモデル化する
ただ，ブログのPVや収益，経過時間を正確にモデル化するのはめんどくさい，っていうか不可能です．
なぜなら，ブログのPVや収益は，『その時のトレンド』，『スマホの普及率』，『その月の更新記事数』などなど様々なことに起因するため，単純な数式では示せないから．
そこで，話を簡単にするため大胆な前提を複数置いてみることとします．
前提を置くことはよくあることで，さっきも『ウォーキングしてる人の時速は一定』っていう前提を置きました．実際にはウォーキング中の速さは変わるはずですが，計算がめんどくさくなるため一定として考えてます．ブログの数式を求めるときも同じく，単純にしてみましょう
ざっくりとした傾向を見るため，かなり簡単化したモデルを作ることとします．
ということで，計算を楽にするための前提条件を付けていきます．結構雑ですがネタ記事なのでお許しを．
前提条件1. 『PV数と収益は比例関係にある』
いきなり大胆な前提ですが，『1万PVのブログで1万円稼げていたら，10万PVのブログで10万円稼げるよね』っていう理論です．
前提条件2. 『PV数はブログの読者数に比例する』
『読者が1000人いて，それぞれ月に10記事読んでくれれば1万PV，もしも読者が1万人になれば10万PVになるよね』って言う理論です．
この2つの仮定より，『読者数が増えればPVも収益も増える』ということが言えるため，読者数がどのように増えるのかを検証していきましょう．
前提条件3. 『読者数の増加速度は，ブログの読者数と，読者の候補数に比例する』
これは多分何言ってるかわからないと思うので少し解説します．
まず，「読者数の増加速度はブログの読者数に比例する」についてみていきます．
読者数が多いと，ブログをシェアしてもらえる確率が高くなるので，新しい読者が増える速さが早くなります
ただ，「読者数の増加率がブログの読者数だけに比例する」とすると，ねずみ講的に読者が増えていくことになってしまいますが，現実的にそんなことはありえないですよね．
なぜなら，『読者の数が増えると，読者となってくれる候補人数がどんどん減っていく』からです
例えば，数学に興味がある人が1万人いるとして，数学系ブログの読者が1000人いたら，あと9000人が読者になってくれる可能性があるので読者の増加速度は大きいといえます．
しかし，すでに9000人の読者がいた場合，あと1000人しか読者になってくれる可能性がなく，読者の増加速度はかなり小さくなってしまいます．
この2つをまとめると，『読者の増加速度は読者数と読者の候補数に比例する』ということになるわけです．
では，この3つの前提を元に式を立てて解いていきましょう．
※ここから理系大学1年生程度の数学の知識が必要となりますので，結果だけ気になる方はここまでスキップしてください．
式を立てて解く
それでは，先ほどの前提条件を元にして式を立てていきます．
分かりやすいように先ほどと同じ例を使っていきます．
ある時刻\(t\)での数学系ブログの読者数を\(x(t)\)としてみましょう．
数学に興味がある人が\(N\)人いて，実際の読者数が\(x(t)\)人の時，読者の候補数は「\(N-x(t)\)人」となります．
読者の増加速度は，読者数の時間微分\( \frac{dx}{dt}\)で表されるため，『読者の増加速度は読者数と読者の候補数に比例する』を数式にすると，比例定数をkとして， \(\frac{dx}{dt} = k\bigl(N-x(t)\bigr)x(t)\)となるんです．
ここまでくれば，ただの微分方程式なので3年生以上の理系大学生なら誰でも解けるはず．
変数分離して部分分数分解を行った後に積分を実行すれば\(x(t)\)について解くことが出来ます．
対数の性質より，\(\ln{\frac{x}{N-x}} = Nkt + C\)となるので，さらに指数関数に直し，\(x(t)\)について解いていきます．
さて，積分定数Cが残っているのはかっこ悪いので，最後に初期条件を決めて代入してみましょう．
時刻\(t=0\)において\(X_0\)人の読者がいたとします．
それを使えば，\(e^c\)の値が求められるので，代入しちゃえば終了です．
ここまでの流れをまとめると，時間経過によるブログの読者数は以下のようになるというわけですね．
結局どういうこと？
先ほどの理論から，ブログの読者数変化が以下のようになることが示されました．
ただ，「結局どういうことかよくわからん」という人も多いでしょう．
具体的に，『始めの読者数がたった1人かつ，あなたがブログで扱っている分野に興味がある人が1000人いる，比例定数\(k=10^{-5}\)』と仮定してグラフを描画してみます．
するとどうでしょう，ネットなどでよく見る『ブログは最初は伸びないが急に伸びる時が来る』というのが顕著に現れたグラフとなっていますね
多くのブロガーが言う，『最初は伸びにくいから3ヶ月頑張ってみよう』というのは上記のグラフを経験則的に知っているからこそなんです．
ではどうやれば伸びるのか
さて，続けていれば伸びるということは分かりました．
どうすれば早く稼げるようになるのでしょうか？
まず1つは「分野選びをミスらない」ということ．
日本で10人しか興味ない分野について書くよりも1万人とかターゲットが居る分野について書くほうが稼げるというのは当たり前ですが，数式でもきっちり示されています
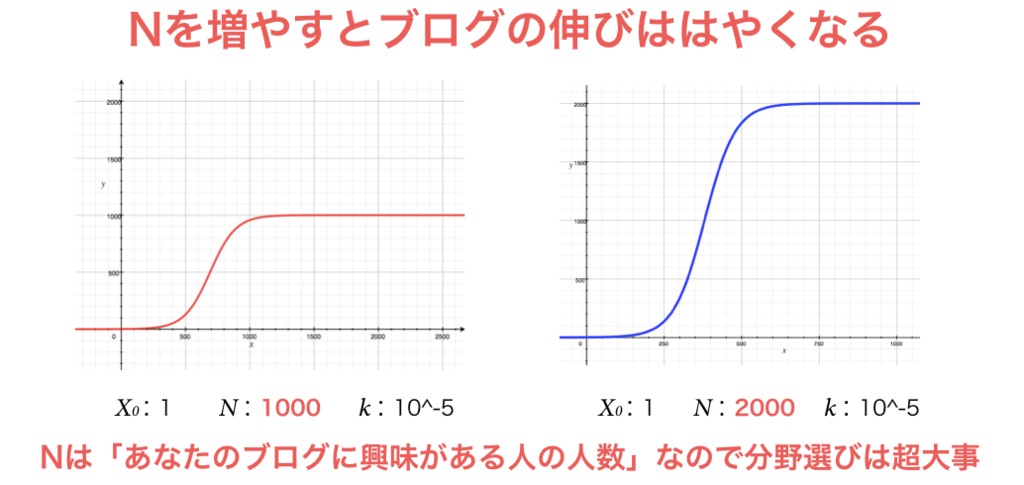
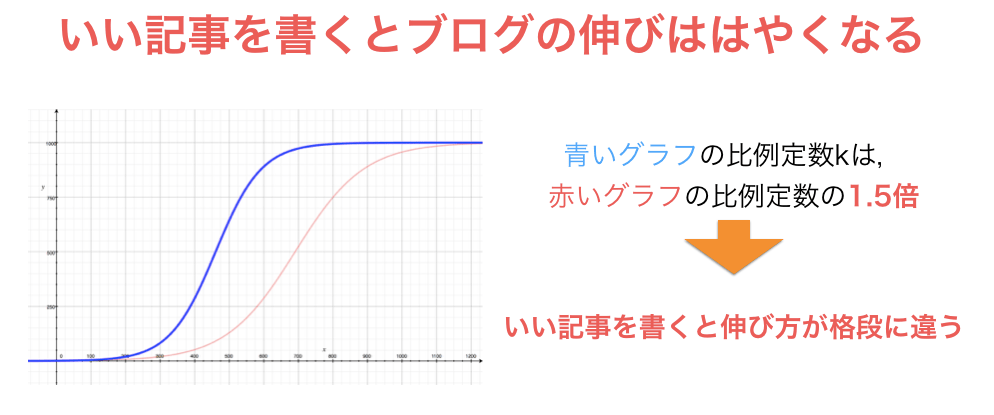
もう1つは，「良い記事を書く」ということ．
比例定数kは記事の書き方や更新頻度によって変わるため，いい記事をたくさん書くことが大前提．
まとめ
今回は，ブログの読者数，PV，収益がどのように変化していくのかについて簡易的な数学モデルを用いて考察してみました．
ブログ論なんてのはネット上に溢れていますが，『分野選定をしっかりして，いい記事を書き続ければぐっと伸びて稼げるようになる』という単純な話です
「数学なんて役に立たない」という人も多いですが，このようにちょっと数学を知っていると『これをした結果どうなるか』という予測が立てやすくなり，近道が出来るというわけ．
『ブログは稼げない』という人も多いですが，結局は初期の伸びない時点で諦めてしまっただけなんです．
続ければ必ず結果が出る．頑張っていきましょう．
- 日本一わかりやすい「経済的自立を果たす人生攻略の10ステップ」（33分23秒）
- 見るだけで売上3倍は確実。「時給10円から年商10億」に至るまでの全ての道のり（39分15秒）
- 有料講演会の内容を公開。最短最速で0→1を立ち上げる起業術（1時間08分35秒）
- 起業初心者へ向けた即金で10万円を稼ぐ具体マニュアル（PDF24ページ）
- 資本主義社会においてお金持ちになる5つのルール（17分36秒）
