こんにちは，学生エンジニアの迫佑樹(@yuki_99_s)です．
畳み込み積分を習った時，誰もがこうは思わなかったでしょうか？
[voice icon=”https://cdn-ak.f.st-hatena.com/images/fotolife/M/McG/20180616/20180616133321.png” name=”迫” type=”l”]
τ-tってなに…
なんでこんなややこしい積分を計算するんだ？
[/voice]
ちなみに，畳み込み積分の定義はこちら．
$$h(x) = \int_{-\infty}^{\infty} f(t) g(\tau-t) dt$$
ということで今回は，つまづきがちな畳み込み積分について詳しく図解してみたいと思います！
畳み込み積分を日本語で言い直してみる
数学語で書くとこうですね．
$$h(x) = \int_{-\infty}^{\infty} f(t) g(\tau-t) dt$$
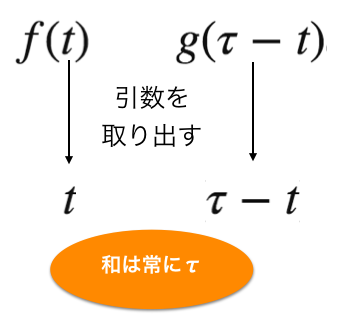
複雑に見えますが，日本語で言い直してみると「引数(関数に渡す値)の和が一定となるような関数の値をかけて積分する」というだけの話なんですよ．
\(f(t)\)と\(g(\tau-t)\)に注目してみましょう．
そうです，つまり単純に，畳み込み積分とは，2つの関数があったら，その引数が一定になるようにしてあげて，それをかけて積分しただけなのです．
これで，畳み込み積分をだいぶ覚えやすくなったのではないでしょうか？
直感的なイメージを考えてみる
たしかに，数式の意味はわかりました．
しかし，この畳込みがどういう意図で使われているのかはわかっていません．
ここで，あるおじさんを投入してみます．
このおじさんは，畳み込み積分を理解するための重要な役割を果たしてくれるおじさんです．
さて，おじさんをピコピコハンマーで叩いてみることにしましょう．(おじさんごめんなさい)
tを日数とした時，t = 3でハンマーで殴られたときの，おじさんの感じる痛みと時間経過を考えてみます．
おじさんはハンマーで殴られることにより，2のダメージを受けるとします．
おそらくですが，1日も経てば痛みもなくなるでしょうから，3日目に殴られて，痛みは少しずつ減っていき，4日にはほぼ痛みがなくなるような，先程のグラフが出来上がります．
いつもいつもハンマーで殴られるとは限りません．
0日目には，バットで殴られたとしましょう．この時は4くらいの痛みを受けることにします．
多分治るのに2日くらい(もっと？)かかるでしょう．
すると，グラフは以下のようになります．
ここで，痛みの特徴として，「時間が経てば痛みは減っていく」という特徴があります．
この特徴により，人は，昔に受けたすごい痛みよりも，最近受けた些細な痛みのほうが辛く感じます．
例えば，3年前の自転車事故よりも，10分前にタンスに小指をぶつけたときのほうが痛いです．
このおじさんも，3日目の状況を見てみると，0日目にバットで殴られた痛みよりも，3日目の当日にハンマーで殴られた痛みのほうが大きいのでしょう．
それを表してるのが下のグラフです．
それでは，これをもう少し数式っぽくしてみましょう．
おじさんが，殴られた瞬間のおじさんが受けた衝撃を\(f(t)\)とします．
例えば，バットで殴られたときは，\(f(t) = 4\)で，ハンマーで殴られたときは，\(f(t) = 2\)ですね．
ここで，\(t\)は殴られた日付です．
t日目に受けた衝撃とでもすればいいでしょう．
f(t)のグラフを書くと，こうなります．
先程は，おじさんが感じていた痛みをグラフにしましたが，今回はおじさんがうけた衝撃なので，殴られた瞬間(t=0,3)以外は0となります．
f(1) = 4, f(3) = 2, f(1.1) = 0, f(2) = 0, f(3) = 0… となるわけですね．
それでは，次に，痛みを和らげる要因を考えてみます．
和らぎはとても単純です．
もちろん，人によってまちまちですが，このおじさんは，半日経てば，痛みが4分の1になると考えます．
なので，バットで殴られたときの衝撃による痛みが以下のように変化するのも納得できると思います．
ハンマーで殴られたときはこうですね．
ここで，痛みの減少の様子をグラフにしてみました．
半日経てば，おじさんの痛みは，もとの25%になっています．
この，痛みの減少は，衝撃を受けてからの経過日数です．
この痛みの減少の関数をg(x)とすると，半日経つと痛みは25%=0.25となるので，g(0.5)=0.25, g(1)=0.0625, などとなります．
ここで衝撃の大きさの関数fと痛みの減少の関数gについて，気をつけておきたいことがあります．
f(x)は，x日目に受けた衝撃です．
g(x)は，衝撃を受けてからx日経過した日に残ってる痛みの割合です．
「x日目」と，「衝撃を受けてからx日経過した日」というのは違いますね．
例を挙げると，「1日目」というのと，「衝撃を受けた1日目から1日経過した日」は違いますよということ．
前者は1日目なのですが，後者は2日目です．
では，これを統一的な書き方で書くとどうなるでしょうか？
衝撃を受けた日を\(t\)日目とします．
そして，現在が\(\tau\)日目だとします．
すると，衝撃を受けた日から現在までに経過した日数は\(\tau – t\)となりますね．
例として，衝撃を受けた日が3日目で，現在が4日目だとしましょう．
つまり，\(t = 3\)，\(\tau = 4\)ということですね．
すると，衝撃の大きさはf(3)なので，以下のグラフより，f(3) = 2であることがわかります．
また，現在までに，g(経過日数分)だけ痛みは減少しているはずです．
現在が4日目で，衝撃を受けたのが3日目なので，痛みは，\(g(4-3) = 0.0625\)に減少しています．
つまり，3日目に受けた痛みは，4日目には0.0625倍になっているので，3日目に2の痛みを受けると，4日目にはわずか2×0.0625で0.125になっていると．
ここまでのことを整理してみます．
\(t\)日目にある量の衝撃を受け，その痛みが\(\tau-t\)日経過後の\(\tau\)日目には，\(f(t) f(\tau – t)\)の痛みになっているわけです．
ここで畳み込み積分の式を見てみます．
$$h(x) = \int_{-\infty}^{\infty} f(t) g(\tau-t) dt$$
つまり，これは痛みを積分してるわけですね．
\(-\infty\)から\(\infty\)まで積分する… 今まで感じてきたすべての痛みを足し合わせているんですね．
とっても簡単に言うと，畳み込み積分っていうのは，おじさんが感じてきた痛みの総合なんです．
直感的なイメージが出来たでしょうか？
なぜ制御工学でよく出るの？
では，なぜ制御工学でよく使われているのかを考えてみます．
制御工学では，「入力によってシステムがどのような状態になるか」を見る機会がとても多いです．
例えば，「アクセルを踏む」という入力により，「車が100km/hで動く状態になる」といったように，ある入力により状態が変化するのです．
今回上げた例では，「おじさんを殴る」という入力により，「おじさんが〇〇っていう痛みを持つ状態になる」といったように，入力で状態を変化させました．
さっき上記で挙げたネタみたいな例も，制御ぽく言おうと思えば言えるんですね．
おじさんに衝撃を与えると，時間が経つに連れておじさんの痛みが減っていきます．
車も，一瞬アクセルを踏み込むと，時間が経つにつれて速度が落ちていきます．
どうでしょう，今回の例がちょっとは制御工学で使えるかも？って思えたんではないでしょうか．
長時間お疲れ様でした．
- 日本一わかりやすい「経済的自立を果たす人生攻略の10ステップ」（33分23秒）
- 見るだけで売上3倍は確実。「時給10円から年商10億」に至るまでの全ての道のり（39分15秒）
- 有料講演会の内容を公開。最短最速で0→1を立ち上げる起業術（1時間08分35秒）
- 起業初心者へ向けた即金で10万円を稼ぐ具体マニュアル（PDF24ページ）
- 資本主義社会においてお金持ちになる5つのルール（17分36秒）
