理工系の学部に進めば,電気回路やら制御工学やらいろいろなところで出てくるラプラス変換.
私の所属するロボティクス学科では2回生前期の微分方程式の授業で出てきました
わかってしまえばシンプルな概念なのに,意外とわかっていない人が多いのも事実なんですよ.
そんな人たちのために,一旦まとめてみたいと思います!
ラプラス変換って何?
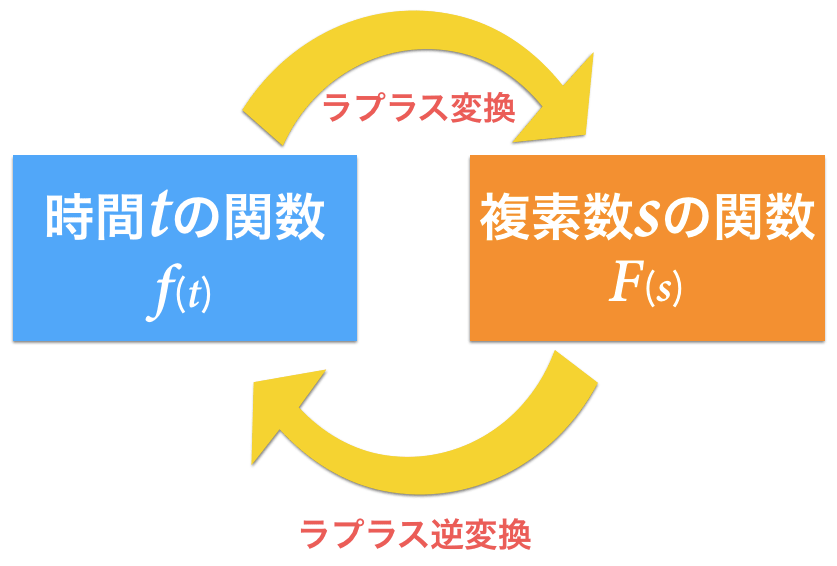
とても簡単に説明すると,時間\(t\)の関数と複素数\(s\)を行き来するための変換です.

私達が実際に生きているこの世界は,時間の経過によって様々なものが変化するため,時間の関数となって表現できるものが多いわけです.
様々な微分方程式などを解こうとすると,処理がめんどうな数式が現れます.
処理がめんどうならば,それを簡単に処理できる形に変形できればよいのではないかと考えた方がいました.
つまり,時間\(t\)の関数のまま計算するととても複雑になるため,それをラプラス変換という変換を用いて複素数\(s\)の関数で表すことによって計算を簡単にしているというわけです.
その変換がラプラス変換ということ.
ラプラス変換の計算
それでは,ラプラス変換をすることによってどれだけ計算が簡単になるのかを見て実感してみましょう…
と言いたいところですが,まずはラプラス変換がどのようなものかを少しだけ知っておく必要があります.
ラプラス変換は見た目は少し複雑な形をしています.
先程,ラプラス変換は\(t\)の関数を\(s\)の関数で表すと言いました.
そこで,変換する前の関数を\(f(t)\),変換後の関数を\(F(s)\)とします.
すると,\(F(s)\)は以下のようになります.

少しだけ難しそうに見えますが,そんなことはありません.
\(f(t)\)に\(e^{-st}\)をかけてあげて,0〜∞でtについて積分したら終わりです.

具体例
それでは,具体例を見ていきましょう.
実際に,\(f(t)=1\)っていう関数をラプラス変換してみましょう.
ではこれをラプラス変換するときは,上で言ったように,\(f(t)\)に\(e^{-st}\)をかけてあげて,0〜∞でtについて積分したら終わりですね.
さぁやってみましょう.
\(f(t)\)が今回1なので,\(f(t)\)に\(e^{-st}\)をかけても,\(e^{-st}\)のままですね..
それを0〜∞でtについて積分するといいだけなので,ラプラス変換後の\(F(s)\)は…
このようになります.

なるほど,つまり1をラプラス変換すると\(\frac{1}{s}\)になるわけですね.
計算自体はそこまで難しいものではないことがわかったと思います.
ここまできて浮かんでくる疑問が… 「で,なんでラプラス変換すると嬉しいの?」
それを次で解説してみます.
ラプラス変換できると嬉しいこと
うちの大学教授が言ってました.
[voice icon=”https://cdn-ak.f.st-hatena.com/images/fotolife/M/McG/20180614/20180614112223.png” name=”教授” type=”l”]
便利さがわからないのは知らないからだ
つべこべ言わずにやりなさい
[/voice]
そんなこと言われてもラプラス変換をして何が嬉しいのかわからなかったらどうにも…
とりあえずでもまぁもう一つくらい例を出してみましょう.
では次に,\(f(t)=t\)っていう関数をラプラス変換してみます.
先程と同じく,「\(f(t)\)に\(e^{-st}\)をかけてあげて,0〜∞でtについて積分したら終わり」を素直にやってあげましょう.
ここで出てきたこの積分,\(\int_0^{\infty} t \times e^{-st} dt\) 大丈夫でしょうか?
高校で習った部分積分を使えば解けますので,少しでも「あれ?」ってなった方は調べてみてください.

つまり,\(f(t)=t\)をラプラス変換すれば\(F(s)=\frac{1}{s^2}\)になるわけです.
なるほど…?
少し整理してみましょう

ほおほお? ここで出てきた1とtっていうものは,微分積分の関係にありますよね.

また,変換された,sの関数はお互いにこのような関係になっています.

みえてきましたか?
\(t\)を変数として使っていた世界では積分として扱われていたものが,\(s\)の世界では割り算として扱うことができます
そして,\(t\)を変数として使っていた世界では微分として扱われていたものが,\(s\)の世界では掛け算として扱うことが出来たというわけです.
計算の手間は圧倒的に減るのではないでしょうか?
つまり,\(t\)の関数では微分や積分がとてもめんどくさかったものなどを,\(t\)の関数をラプラス変換し,得た\(s\)の関数を掛け算や割り算で簡単に計算し,ラプラス逆変換をすることによって\(t\)の関数に戻せば,手数は増えますが計算の手間自体は減るということですね.

なんと,2階微分を\(s\)を2回かけるだけ,3階微分を\(s\)を3回かけるだけというように微分が掛け算で簡単に計算できるわけです.
ちゃんとした証明
では本当に微分が掛け算になるのかを計算してみましょう.
\(f(t)\)という関数について考えてみましょう.この\(f(t)\)を微分すると,当たり前ですが\(f'(t)\)になりますね.
ではこの\(f'(t)\)を実際にラプラス変換してみて,\(f'(t)\)という微分の形がなくなって,\(s \cdot F(s)\)という形が出てきてくれたら,「微分を掛け算の形に直せる」という上記の仮説が正しいといえますね
ではやってみましょう.
ラプラス変換の方法は… そうです,先程から何度もやっているように「ラプラス変換したい関数に\(e^{-st}\)をかけてあげて,0〜∞でtについて積分」を行います.
まず,今回ラプラス変換したい関数は\(f'(t)\)なので,まずはそれに\(e^{-st}\)をかけます.
すると,\(f'(t)e^{-st}\)となります.
あとはこれを部分積分を使って積分していきましょう.

なんと,微分が式中から消えて\(s \cdot F(s)\)という掛け算の形が出現しました.
どうでしょう? \(t\)の世界での微分が\(s\)の世界だと掛け算で表すことが出来るっていう意味が分かったでしょうか?
実はこれラプラス変換の微分法則っていう大層な名前がついてるんですが,簡単に言うと微積がめんどい人が掛け算割り算で代用できるようにした手法です.
まとめ
他のサイトや書籍のように,ひたすらラプラス変換を計算するのではなく,「なんでこんなことするの?」という視点からのアプローチでした.
ここでしつこいように言ってきました,ラプラス変換したい関数に\(e^-st\)をかけてあげて,0〜∞でtについて積分を計算すればラプラス変換は出来ます.
その計算過程で詰まったら,ネット上にいくらでも計算方法は転がっているのでそちらを参考にしてみてください.
実際ラプラス変換の定義から実際に計算してみることをおすすめしますよ
他にもラプラス変換に関してはいろいろな法則がありますが,とりあえず基礎はこんな感じです.
長文をお読みいただきありがとうございました.