まずは論理回路の話
みなさん,コンピュータがどのようにして動いているか,ご存知でしょうか.
とってもざっくりした説明をすると,電気のオンオフでコンピュータは動いているんですね.
電気が流れているか流れていないかの組み合わせによってコンピュータは動作を決めているわけです.
このオンオフで計算させたり,論理演算をさせる回路を論理回路っていいます.
論理演算って?
まずは,論理演算とはなにかという話です.
論理演算とは、2つ以上の1または0入力値に対して、1つの演算結果(1または0)を出力する演算のことである。
なるほど?
よくわかりませんね.
簡単に言うと,「真」と「偽」の2つを使っていろいろなものを表してみよう!っていうことです.
例えば,論理演算の1つであるAND演算というものは,ANDという名の通り,2つ以上の条件の2つともが真の時だけ真になる演算のことです.
例えば,「私は大学生です」と「私は関西に住んでいます」という2つの条件があったら,そのAND演算は「私は大学生かつ関西に住んでいます」となります.
演算した結果の,「私は大学生かつ関西に住んでいます」を満たすには,「大学生」という条件と「関西に住んでいる」という2つの条件を満たす必要がありますね.
このように,2つ以上の演算に対して1つの結果を返すことを論理演算といいます.
コンピュータの世界では,「真」を1,「偽」を0と表すことが多く,「1かつ1は1」とか「1かつ0は0」とか言ったりします.
NAND回路って?
で,今回の主人公はNAND回路と呼ばれるものです.
NAND回路のなにがすごいかっていうと,すべての論理演算はNAND回路を組み合わせればできるということです.
AND回路が,1と1が入力された時だけ1を出力していた回路でした.
NANDとは,Not ANDのことなので,ANDを反転した結果がでます.
先ほどの例で言うと,「私は大学生です」と「私は関西に住んでいます」という2つの条件があったら,そのNAND演算は「私は大学生でないかつ関西に住んでません」となりますね.
「私は大学生でないかつ関西に住んでません」を満たすには,条件1の「私は大学生です」が偽(0)かつ「私は関西に住んでいます」が偽(0)の時だけ「私は大学生でないかつ関西に住んでません」が真(1)になります.
よって,NAND回路は下の真理値表のように,1と1入力された時にだけ0を出力する回路です.

そして,これがそのNANDゲートというものを表す記号です.

それでは,ここから実際に様々なものを作っていきましょう.
NOT回路を作る
入力に対して反転させる回路です.

入力A,Bに1,1を与えると0を出力,入力に0,0を与えると1を出力するNANDの特性から,以下のようにNAND素子に入力を与えればNOT回路が作成できます.

実際に作ってみました.今回,LEDを出力として使用し,真(1)の時だけ点灯するようにしてみました.入力はボタンを使用し,押された時に真(1),推されてない時に偽(0)と考えることにし,擬似的に論理回路を再現しています.
このように,押している(入力が1)の時にLEDが消える(出力が0),話している時(入力が0)の時にLEDがつく(出力が1)となっているのがわかります.

AND回路を作る
次にAND回路です.
AND回路は,例のところでも説明しましたが,入力A,Bがともに1の時だけ1を出力する回路です.

NANDがNot ANDの略でAND回路を反転させたものなので,AND回路を作りたければ逆にNANDの出力を反転させればいいです.
出力を反転させるには,先ほど作ったNOTを組み合わせればいいですね.
ということで,NANDの出力をNOTを使って反転させましょう.
このような回路図になります.

実際に作ってみた結果がこちらです.

どっちのボタンも押してない時(入力が2つとも0)や,片一方だけをおした時(片一方の入力だけが0)ではLEDは点灯しませんが,両方おした時だけLEDが光って1を出力していることがわかります.
OR回路を作る
OR回路は,入力A,Bのどちらか1つでも1が入力された時に1を出力する回路です.

NAND回路の真理値表をよく見ると,OR回路に変えるためには,0,0が入力されたの時の出力を0にし,1,1が入力された時の出力を1に変えればいいということがわかります.
現在,0,0が入力された時の出力は1で,1,1が入力された時の出力は0なので,入力をそのまま反転させてやればいいでしょう.0,1が入力された時の出力は,入力を反転させたとしても変わらないので,NAND回路の入力を反転させることによってOR回路を作ることができます.

実際に作ってみた回路がこれです.
両方共ボタンを押していない時はLEDは光りませんが,片一方どっちかでも押されていたらLEDが光っていることがわかります.

XOR回路を作る
次にXOR回路と呼ばれるものです.
XORは,排他的論理和と呼ばれるのですが,「2つの入力が異なっていた時だけ真を返す」というちょっと変わった論理回路です.

これもNAND4つ使えば作ることができてしまうんです.
回路図はこのようになっています.

少しややこしいですが,入力を与えた時,各NANDゲートがどのような値を返すのかを一つづつ確認していくと正しいことがわかります.
実際に作ってみた回路がこちらです.

どうでしょうか,AとBが異なる入力の時にだけLEDが点灯しています.
多数決回路を作る
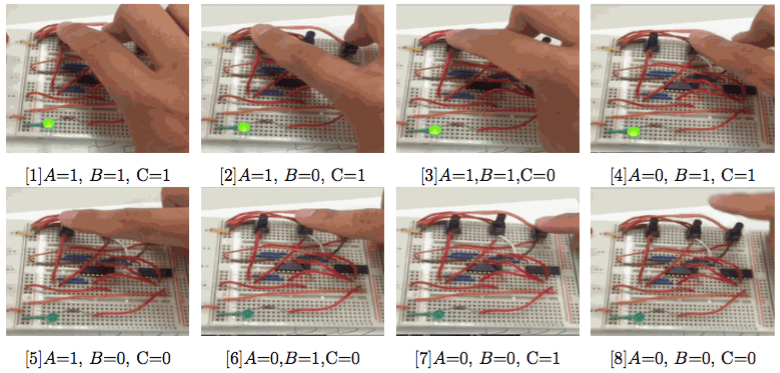
多数決回路とは,3つの入力を与えた時に,2つ以上が1だったら1を出力する回路です.
名前の通り多数決をすることができる回路ですね.
真理値表は以下のようになっています.

今までは入力が2つだったので2入力NANDと呼ばれるものを使用していましたが,今回は多数決をするということで3つの入力が必要となります.
3入力NANDと呼ばれる,3つの入力全てが1と時のみ0を出力するという素子を使用しました.
3入力NANDは,「3つの入力の全てが1の時のみ0を出力する回路」で,2入力NANDが,「2つの入力の全てが1の時のみ0を出力する回路」.
この特性をうまく利用することによって,入力A,B,Cのうち,0個,もしくは1個しか1が入力されていなければ3入力NANDは0を出力し,2個,もしくは3個1が入力されていれば3入力NANDは1を出力するという回路を作ることができます.
これらを使って作った多数決回路がこちらです.

実験してみると,確かに2つ以上おした時に光っているのがわかります.

実験をやってみて
このように,NAND素子だけで様々なものを作ることができることがわかります.
コンピュータの演算も,これを応用して出来ていると考えればすごいですよね.
実際にこうやって回路を組んでみると,とても複雑に見えるコンピュータのCPUとかもすこーーーしだけ身近に思えます.
実際に手を動かすことで理解も深まり,楽しい実験でした.